QuickSort C++ is one of the fastest sorting algorithm in programming. Quick Sorting works on divide and conquer approach. It sorts the array in such a way so that the pivot point comes into the middle and at the left of the pivot point smaller elements are generated and at the right of the pivot point larger elements are generated. It is preferred on Merge Sort, insertion sort, selection sort and bubble sort. When we work with arrays, sometimes we have to deal with massive data, due to which it takes a lot of time in searching and sorting. Here we will use C++ Quick Sorting in order to discuss sorting of arrays in C++. QuickSort is preferred on Merge Sort because it has a smaller constant factor. In this tutorial we will discuss in detail the working of C++ quicksort, we will discuss its running time, its advantages and disadvantages, and when we should use it. We will make quick walk through with proper examples, so you could understand the working of Quick Sort.
Example of QuickSort Algorithm:-
QuickSort(A, p, r) If (p < r) q= Partition(A, p ,r) QuickSort(A, p, q-1) QuickSort(A, q+1, r) ......................................... Partition(A, p, r) i= p-1 PE= A[r] for(j=p to r-1) if A[j] <= PE --------i = i+1 --------exchange A[i] with A[j] exchange A[i + 1] with A[r] return i+1
Explanation of QuickSort C++ Algorithm:-
Let’s take an example of an Array A = {2, 3, 1, 8, 10, 14, 12, 9}, now we will apply Quick Sorting on array of eight elements and discuss its working.
Now we will talk in terms of indexes, remember that point throughout the tutorial.
First Pass:-
p = 1 and r= 8, therefore the condition p<r becomes true, now function Partition will be call.
Here i= 0, p=1, r=8 and PE=9. Remember one thing, we are talking about in terms of indexes for all the variables except PE, because PE stores a value at index r.
Now control will transfer to the For loop. The loop will run from (j=p to r-1).
First iteration:-
Here i=0, p=1, j=1, r=8 and PE=9.
A[j] <= PE –> 2<=9 –> true.
Therefore, we will increment in i.
Now i= 1.
We will exchange A[i] with A[j] –> A[1] with A[1].
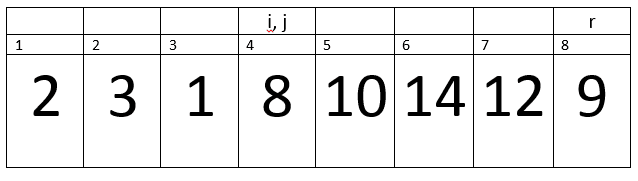
Second Iteration:-
Here i=1, j=2, PE=9.
A[j] <= PE –> 3<=9 –> true.
Therefore, we will increment in i.
Now i= 2.
We will exchange A[i] with A[j] –> A[2] with A[2].
Third Iteration:-
Here i=2, j=3, PE=9.
A[j] <= PE –> 1<=9 –> true.
Therefore, we will increment in i.
Now i= 3.
We will exchange A[i] with A[j] –> A[3] with A[3].
Fourth Iteration:-
Here i=3, j=4, PE=9.
A[j] <= PE –> 8<=9 –> true.
Therefore, we will increment in i.
Now i= 4.
We will exchange A[i] with A[j] –> A[4] with A[4].
Fifth Iteration:-
Here i=4, j=5, PE=9.
A[j] <= PE –> 10<=9 –> False.
So, loop will continue.
Sixth Iteration:-
Here i=4, j=6, PE=9.
A[j] <= PE –> 14<=9 –> false.
Loop will continue.
Seventh Iteration:-
Here i=4, j=7, PE=9.
A[j] <= PE –> 12<=9 –> False.
Loop will continue.
Eighth Iteration:-
Condition becomes false, therefore Loop will terminate.
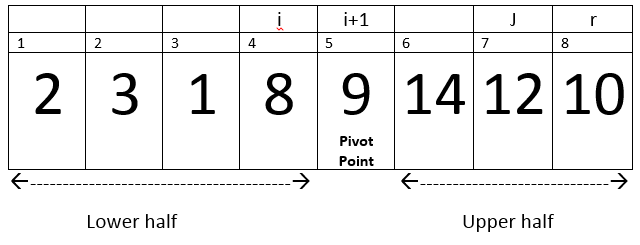
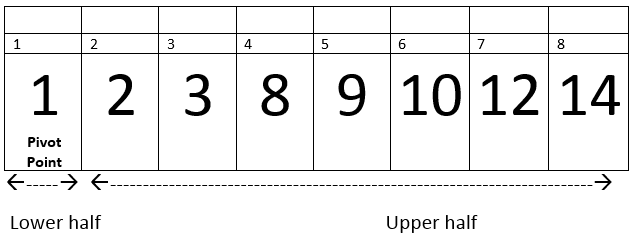
Hence control will transfer to the next statements. That is exchange A[i + 1] with A[r] –> A[5] with A[8]. After Exchange the array will looks like:-
As you can see by the above example, the C++ quicksort have divided the array into three parts that is the pivot point, lower half and upper half.
Now the function will return the value of Pivot Point –> 5.
Therefore, now q = 5 and next statements will execute.
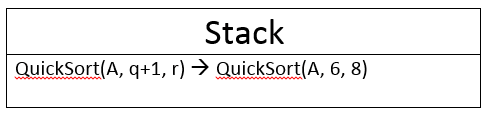
QuickSort(A, p, q -1) –> QuickSort(A, 1, 4)
QuickSort(A, q+1, r) –> QuickSort(A, 6, 8)
Now the thing to remember, whenever partition function will called the pivot point will become sorted, Statements after the recursion are pushed into the stack.
Running time of C++ QuickSort Algorithm:-
Now we will discuss the running time of the quickSort C++.
Worst Case:-
The worst case will occur, if array does not divide into equal parts, like in a ratio of 1:9. If we talk about the above example then if we took Pivot Point = 1 then array will divide into two parts but one part consist upon only one element and the other part consists upon eight elements. The run time of worst case is n2.
E.g
Average Case:-
In average case, the array divides into the ratios of 2:8, 3:7, 4:5, the run time of average case in nlogn. Mostly 90% of the time average case occurs.
Best Case:-
In best case, the array is always divides into two equal halves. Its running time is nlogn.
QuickSort Example implementation in C++:-
I will soon published quick sort C++ implementation code.
If you have any questions then post them into our forum or in a comment section of this post.

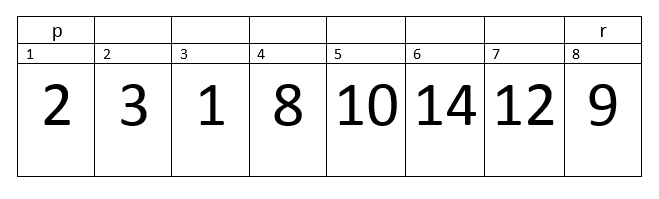
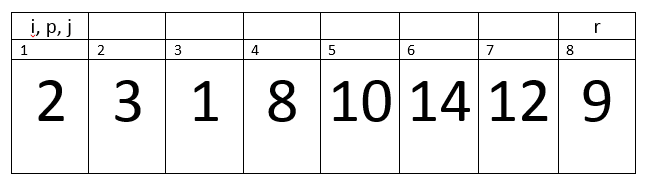
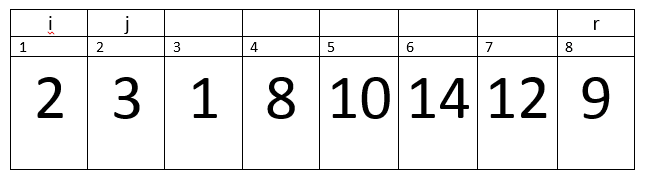
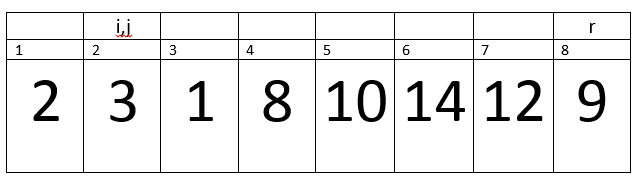
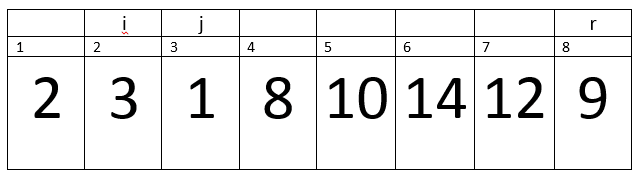
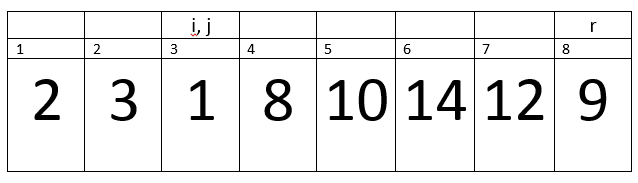
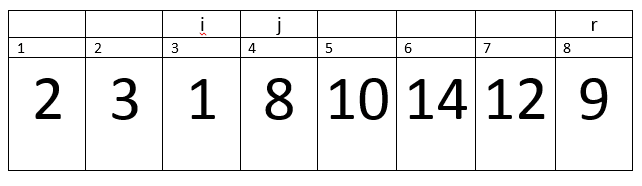
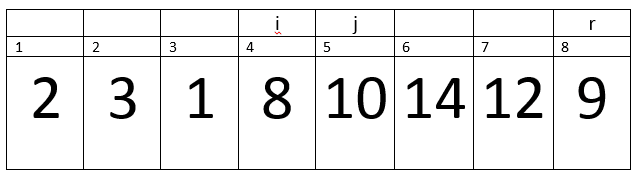
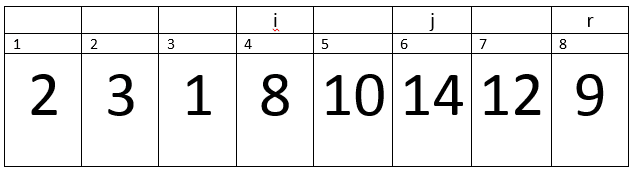
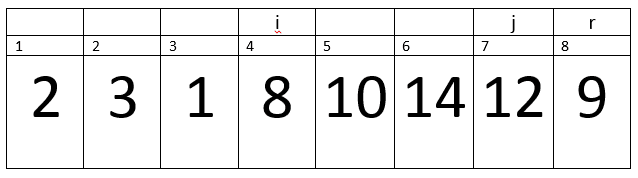



Your C++ code has been treated as HTML code!
thanks for pointing out !!!