Home » C++ » Bubble Sort in C++ with examples

C++

Bubble Sort in C++ with examples

royal52

Jun 17, 2024

10156 Views 16 comments

SaveSavedRemoved 0

we will see the working and operations of bubble sort in C++ with proper examples by the sorting of arrays.

Sorting of Arrays:-

The process of arranging the arrays in ascending order or descending order is called Array sorting.

Bubble Sort:-

Bubble sorting is the very commonly and widely used sorting technique in C++ programming. It is also known as the exchange sort. It repeatedly visits the elements of an array and compares the two adjacent elements. It visits the array elements and compare the adjacent elements if they are not in the right order then it puts them into the right order. It continues to swap the elements until no more swaps are required, which means the given array is sorted. It works in the following steps described below:

1. It will compare two adjacent elements, if second element is smaller than the first then it will swap them, if we wanted to sort an array in an ascending order.

2. It will continue the above process of comparing pares, from the first pare to the last pair, at its first iteration the greatest element is placed at the last index of an array.

3. Then it will again repeat the above steps for all the elements by excluding the greatest one.

4. It will continue to repeat until the array becomes sorted.

Let’s take a look towards the following example which will illustrate and completely describe the use, working and operations of bubble sort in C++.

Example of Bubble Sort:-

#include <iostream>

using namespace std;

int main()
{
    
    
 int hold;
 int array[5];

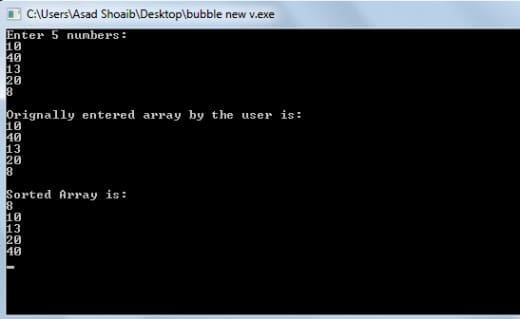
 cout<<"Enter 5 numbers: "<<endl;

 for(int i=0; i<5; i++) 
 { 
  cin>>array[i];
 }

 cout<<endl;
 cout<<"Orignally entered array by the user is: "<<endl;

 for(int j=0; j<5; j++)
 {
  cout<<array[j];
  cout<<endl;
 }

 cout<<endl;

 for(int i=0; i<4; i++)
 {
  for(int j=0; j<4; j++) 
  {
   if(array[j]>array[j+1])
   {
    hold=array[j];
    array[j]=array[j+1];
    array[j+1]=hold;
   }
  }
 }

 cout<<"Sorted Array is: "<<endl;

 for(int i=0; i<5; i++)
 {
  cout<<array[i]<<endl;
 }
    

    return 0;
 }

Explanation:-

Now this program will be explained with proper example.

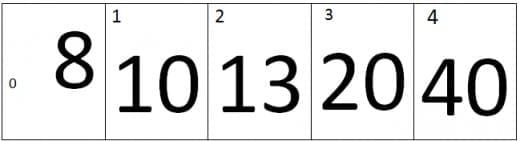
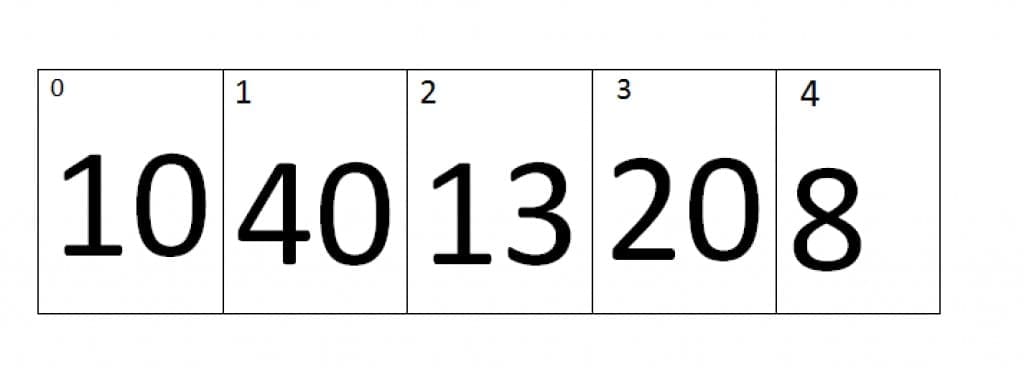
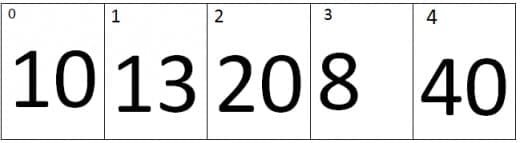
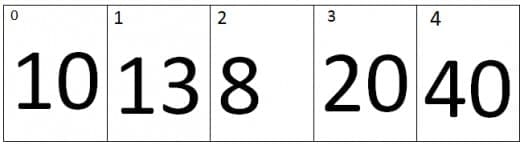
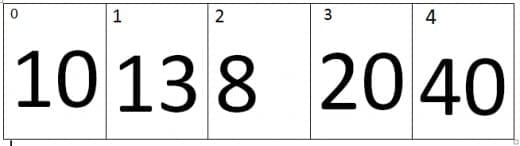
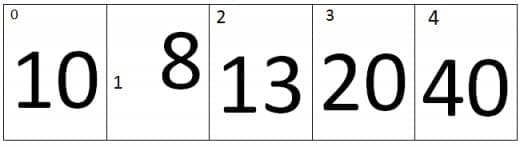
Just consider the array entered by the user is:

Now the program will use a nested loop to perform sorting. The iterations of outer loop will specified the number of passes and the inner loop will specify the number of iterations.

At the beginning when the loop begins, the value of i=0, Therefore first pass is started.

First Pass:

In first pass the value of i=0 and the inner loop came into action, it will perform 4 iterations and check the condition of the following block of statements.

if(array[j]>array[j+1])
   {
    hold=array[j];
    array[j]=array[j+1];
    array[j+1]=hold;
   }

Iteration no. 1:

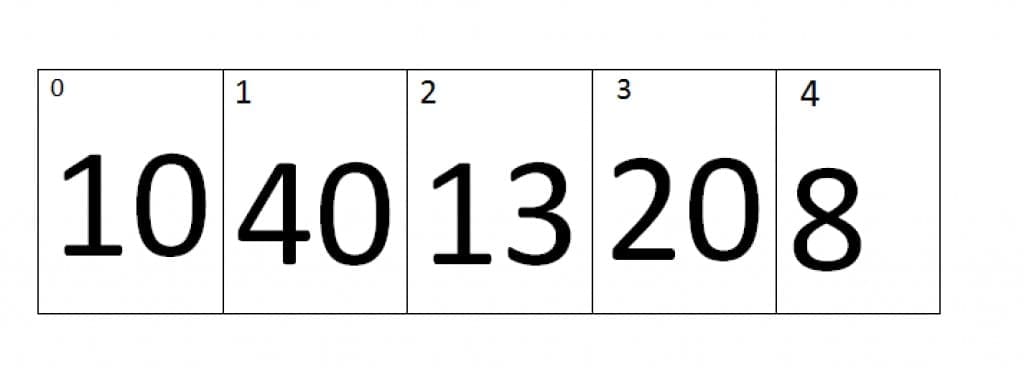
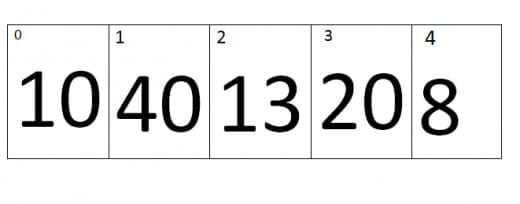
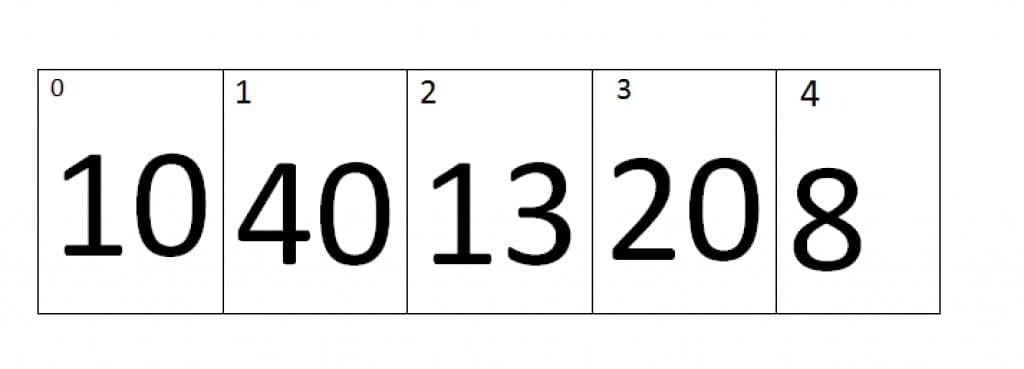
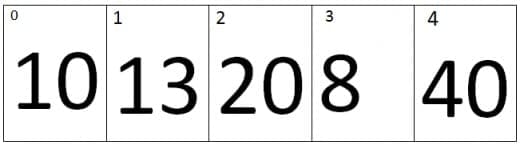
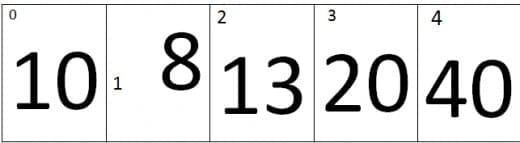
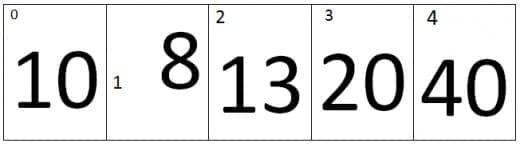
At first iteration the value of j=0 and the value of j+1=1, Therefore it will compare the values of zero index and the first index of an array. As we can see that the value at Zero index is smaller than first index, therefore the array remains the same.

Iteration no.2:

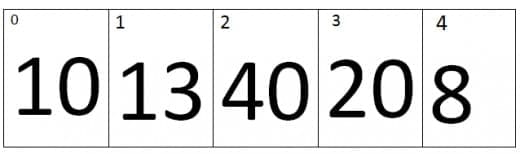
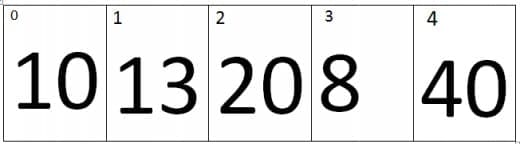
At second iteration the value of j=1 and the value of j+1=2, Therefore it will compare the values of first index and the second index of an array. As we can see that the value at second index is smaller than first index, therefore the elements of first and second index will be swap, the new array looks like.

Iteration No.3:

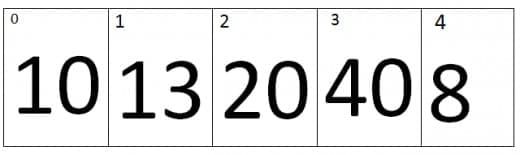
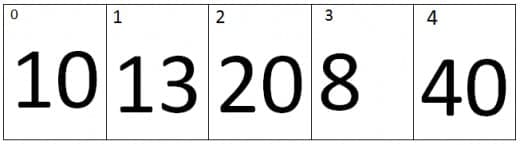
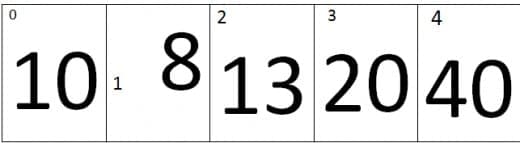
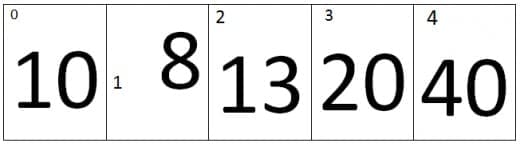
At Third iteration the value of j=2 and the value of j+1=3, Therefore it will compare the values of second index and the Third index of an array. As we can see that the value at third index is smaller than second index, therefore the elements of third and second index will be swap, the new array looks like.

Iteration no.4:

At fourth iteration the value of j=3 and the value of j+1=4, Therefore it will compare the values of third index and the fourth index of an array. As we can see that the value at fourth index is smaller than third index, therefore the elements of fourth and third index will be swap, the new array looks like.

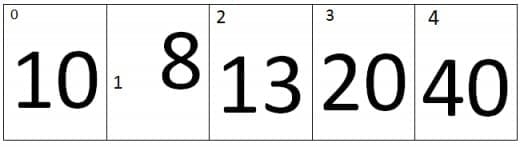
As you can see that at the end of the first pass the largest value is placed at the last index.

Second Pass:

Iteration no. 1:

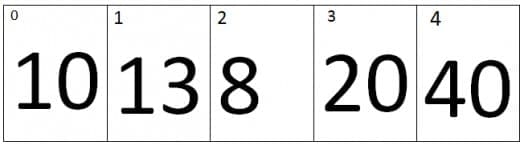
At first iteration the value of j=0 and the value of j+1=1, Therefore it will compare the values of zero index and the first index of an array. As we can see that the value at Zero index is smaller than first index, therefore the array remains the same.

Iteration no.2:

At second iteration the value of j=1 and the value of j+1=2, Therefore it will compare the values of first index and the second index of an array. As we can see that the value at second index is greater than first index, therefore the array will be same.

Iteration No.3:

At Third iteration the value of j=2 and the value of j+1=3, Therefore it will compare the values of second index and the Third index of an array. As we can see that the value at third index is smaller than second index, therefore the elements of third and second index will be swap, the new array looks like.

Iteration no.4:

At fourth iteration the value of j=3 and the value of j+1=4, Therefore it will compare the values of third index and the fourth index of an array. As we can see that the value at fourth index is greater than third index, therefore the array will remains the same.

As you can see that at the end of the second pass the second largest element is places at the second last index of an array.

Third Pass:

Iteration no. 1:

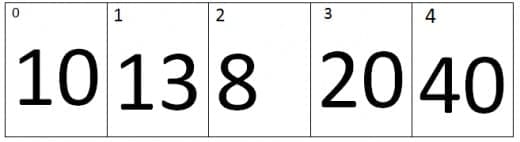
At first iteration the value of j=0 and the value of j+1=1, Therefore it will compare the values of zero index and the first index of an array. As we can see that the value at Zero index is smaller than first index, therefore the array remains the same.

Iteration no.2:

At second iteration the value of j=1 and the value of j+1=2, Therefore it will compare the values of first index and the second index of an array. As we can see that the value at second index is smaller than first index, therefore the elements will swap and new array will be look like.

Iteration No.3:

At Third iteration the value of j=2 and the value of j+1=3, Therefore it will compare the values of second index and the Third index of an array. As we can see that the value at third index is greater than second index, therefore the array remains the same.

Iteration no.4:

At fourth iteration the value of j=3 and the value of j+1=4, Therefore it will compare the values of third index and the fourth index of an array. As we can see that the value at fourth index is greater than third index, therefore the array will remains the same.

As you can see that at the end of the third pass the second largest element is places at the third last index of an array.

Fourth Pass:

Iteration no. 1:

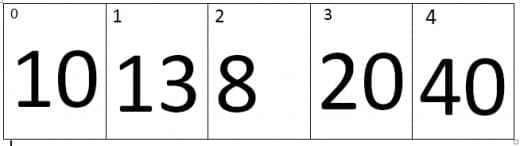
At first iteration the value of j=0 and the value of j+1=1, Therefore it will compare the values of zero index and the first index of an array. As we can see that the value at Zero index is greater than first index, therefore the elements will swap and new array will be look like.

At this point the loop is completed and the fourth last value is placed at the fourth last index of an array. Which means the position of fourth value is final, the position of fifth value is automatically finalized because it automatically placed at index one. Now at the end outer loop will also terminate and we will get the perfectly sorted array in ascending order with the help of Bubble sort technique.